引言
压滤机因其得到的滤饼含水率低,并能实现全自动间歇操作,故已在矿山,轻工,化工等行业得到广泛地应用。通常压滤机的设计和操作都是以Ruth过滤公式为基础进行的。但是,固液混合物的脱水一般由过滤和过滤压密2个阶段组成,过滤阶段服从Ruth过滤公式⑴,而过滤压密阶段则与之不符,该阶段所占时间有时高达整个操作时间的70%⑵。因此,只按Ruth过滤公式设计的压滤机,往往达不到生产要求(滤液量减少或滤饼湿含量过高)。
厢式压滤机的一个操作周期为总的脱水时间和滤机停机时间(卸除滤布、清洗滤布和重装滤机所需的时间,称之为辅助时间)的总和。一般来说,辅助时间与压滤机的结构、滤浆的性质、自动化机构的应用程度有关。如果上述条件已定,就可认为辅助时间是与压滤机的生产能力无关的一个常数。对于某一个特定的辅助时间,分析与计算固液分离中2个阶段所需的时间,就可以得出最佳过滤时间的大小;相应地,压滤机达到最大生产能力时的操作条件也能快速而准确的得到。

2厢式压滤机操作过程中相关参数的计算
厢式压滤机的操作具有周期性,除了滤浆输入外,还包括过滤、液力压密、洗涤、滤饼卸除、滤布清洗和重装滤机等。因此,可对一个操作循环进行最佳操作条件的研究。其计算方法有2种,一种把过滤和滤饼压密阶段分开计算,过滤阶段用传统的Ruth公式计算,过滤压密阶段用过滤压密公式计算,其临界点则用临界点公式计算;另一种是把过滤和过滤压密2个阶段合并在一起,用一个压滤方程计算。本文采用第二种计算方法。
2-1压滤阶段
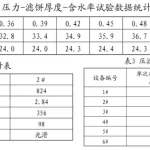
考虑过滤介质阻力,则“由通过压缩渗透试验,求出过滤常数K,3,以及最终滤液体积后,即可得出V和。的关系曲线。
2.2洗涤阶段
此阶段为恒压操作,假设洗水粘度与滤液粘度相等,且洗涤推动力与过滤终了时的压强差相等,洗水体积与滤液体积成正比。
若洗涤压强与恒压过滤阶段压强不同,或洗水粘度与滤液粘度不同,则洗涤时间应重新校正。
3最大生产能力和最佳操作周期
以生产能力最大的操作周期为最佳操作周期,生产能力以单位时间内得到的滤液体积表示。
当压滤机和料浆一定时,以外的其它参数均为常数。因此,通过matlab或其它数值计算软件,就可求出压滤机的最佳过滤时间和相对应的最大生产能力。
4计算举例
用厢式压滤机过滤某种悬浮液,压滤压力F=9.81X105Pa,洗水体积为滤液体积的0.1倍,洗涤压力与恒压过滤阶段的压力相等,洗水粘度和滤液粘度近似相等,最终流出滤液体积为1n?,压滤系数K=7.06X10~6m2/s,过滤介质阻力可以忽略,滤饼压缩特性数B=4.4,辅助时间6d=300s,试确定其最佳过滤时间。
小结
目前,厢式压滤机已经得到了广泛的应用,但对其操作工艺过程的研究大都仅限于按传统的Ruth过滤公式进行。事实上,厢式压滤机的压滤过程中还存在一个偏离Ruth过滤公式的过滤压密阶段,其。与V的关系曲线明显与过滤阶段不同,因此,必须将它们综合考虑,才能得到与实际相符的计算结果。
在前人研究的基础上,将2个阶段的工艺参数统一在整体函数计算式中,准确而方便的计算出最佳操作周期和与之相对应的最大生产能力;而且,当过滤面积一定时,人们总是希望在较低压力下操作,减少能量损耗,降低操作费用和设备费用。因此,本文的研究对于提高压滤机的生产能力,降低能耗具有一定的实用价值,还为这类过滤设备的设计提供了理论依据和指导。

但是在上面公式的应用过程中,有2个问题仍需注意:
在恒压过滤中过滤阶段的变化过程与设备和操作条件有关,难以找到一个普遍的定量关系式表示,因此,在计算中,近似地将整个过滤阶段视为恒压操作。
对于压滤过程的计算是参照中等可压缩物料的实验数据进行的,采用的是Terzaghi模型,忽略了因滤饼压缩而引起的脱水和滤饼的蠕变因素。该因素尤其在高操作压力下影响较大。因此对于高操作压力下,高压缩性滤饼的过滤压缩特性,仍有待今后作进一步的深入研究。
技术:188517-18517
邮箱:suton@su-ton.com
 板框厢式隔膜压滤机
板框厢式隔膜压滤机